Research |
Our research team consists of applied mathematicians, physicists, computer scientists, clinicians, epidemiologists, and social scientists who focus their research activities on the analysis of big data sets to understand and predict the behavior of complex systems. Specifically, we conceive and implement decision-making support tools to address societally relevant problems in the physical, environmental, and health sciences. Examples of the areas of research that we focus on can be explored below and include: Digital Epidemiology, Pandemic Preparedness, Improvement of patient care and hospital resource allocation, Climate and Health, Human Behavior Characterization (via surveys), Global Atmospheric Chemistry Modeling, Computational Fluid Dynamics.
Our work combines the analysis of digital traces and big data sets to conceive data-driven mathematical approaches, and often machine learning-based, to characterize complex systems and to provide solutions to challenging problems. We frequently use high–performance computing environments to implement our models and design dashboards to visualize their output. We also develop scientific computing methodologies, including the numerical solution of (ordinary and partial) differential equations, to solve problems in physical and environmental systems.
Our work combines the analysis of digital traces and big data sets to conceive data-driven mathematical approaches, and often machine learning-based, to characterize complex systems and to provide solutions to challenging problems. We frequently use high–performance computing environments to implement our models and design dashboards to visualize their output. We also develop scientific computing methodologies, including the numerical solution of (ordinary and partial) differential equations, to solve problems in physical and environmental systems.
Expand
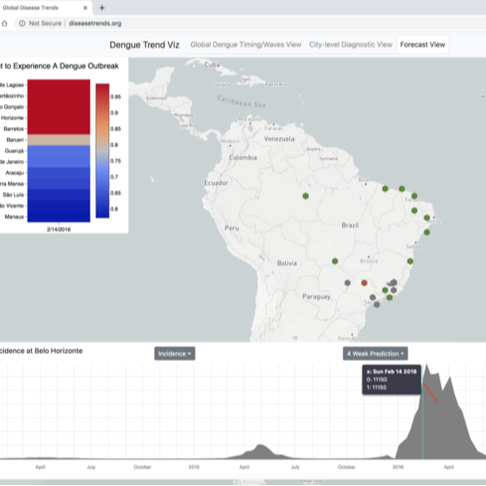
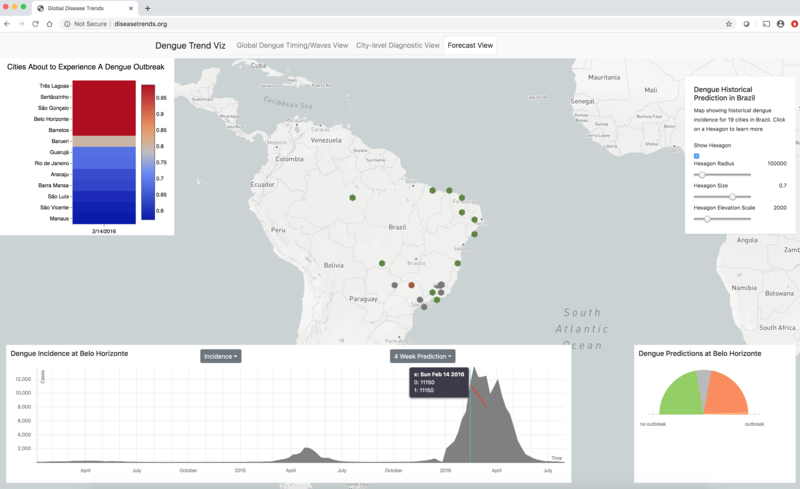
Our team works towards the design and implementation of digital epidemiology tools aimed at monitoring disease outbreaks in real-time. We are constantly developing methodologies that leverage information from multiple data-sources including Google search query patterns, Twitter microblogs, cloud-based electronic health records, weather, and human mobility, to produce real-time and short-term forecast disease activity estimates of pandemic events such as the ongoing COVID-19 and monkeypox pandemics (the 2014 West African Ebola outbreak, the 2014 Latin American Zika outbreak), and endemic disease outbreaks such as dengue fever, influenza and malaria.
Learn more > Figure. We are constantly striving to improve our real-time disease estimates with the goal of assisting public health officials make informed decisions to mitigate the effects of disease outbreaks. Our platform will soon display disease estimates for Dengue, Flu, and a diverse arrray of emrging outbreaks throughout the world. |
Expand
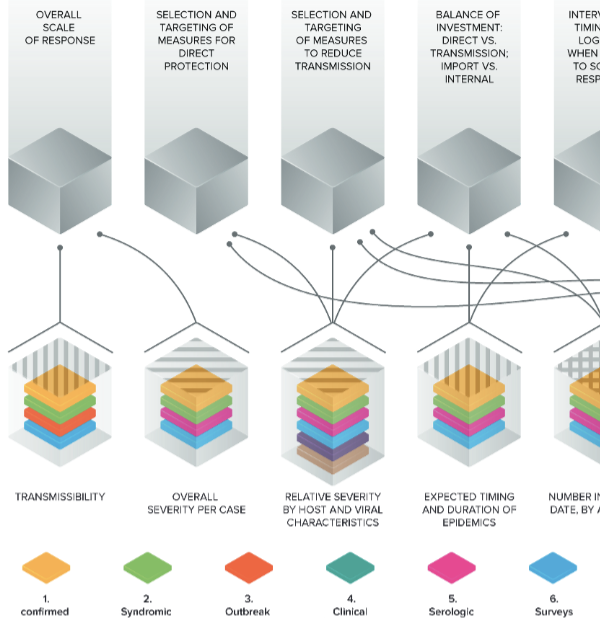
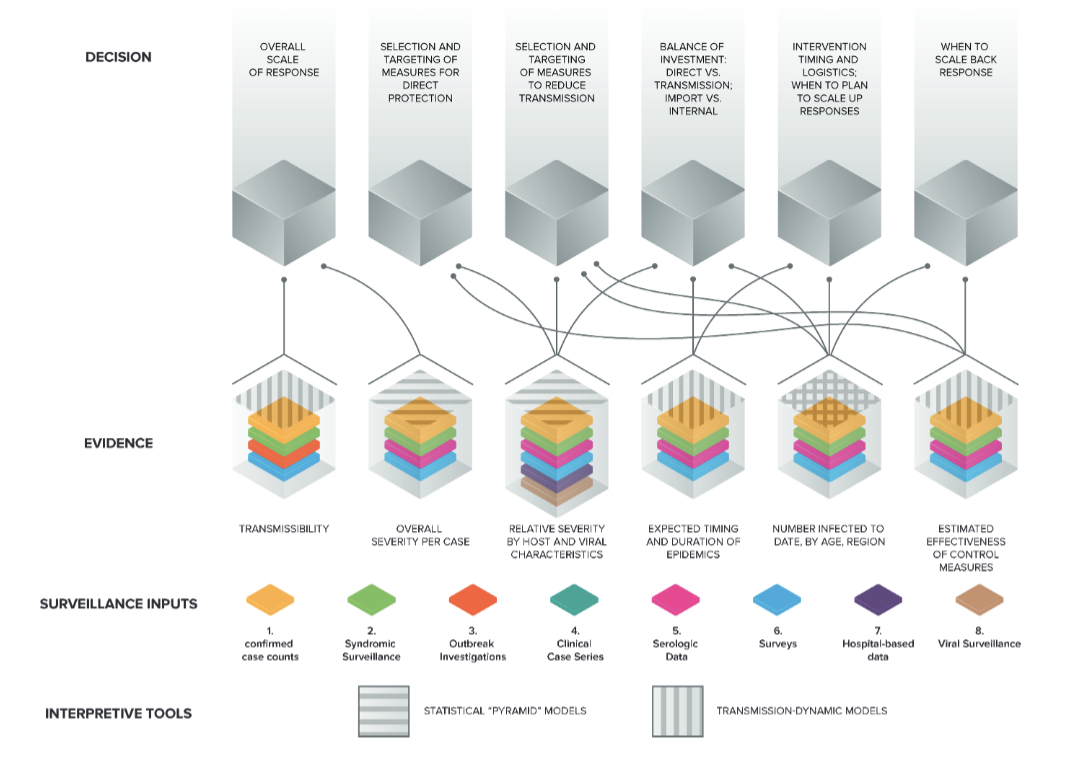
Catastrophic epidemics, when they occur, typically start from localized and far smaller (non-catastrophic) outbreaks that grow into much greater threats. One key bulwark against this outcome is the ability of governments and the health sector more generally to make informed decisions about control measures based on accurate understanding of the current and future extent of the outbreak. Our team works in the design of mathematical strategies to provide decision makers and public health officials with high-quality situation reporting, by providing real-time estimates of key epidemiological quantities (cumulative incidence, effective reproductive number, the likelihood that an outbreak will occur in the near future in a given locations) to help them make informed decisions, leveraging traditional and novel data sources.
Figure Key decisions on pandemic response and the evidence base on which they ideally rest |
Expand
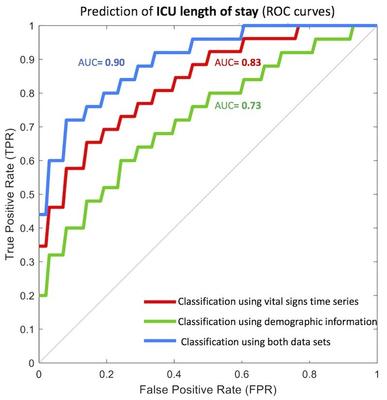
Out team utilizes mathematical concepts of machine learning to improve patient outcomes in Critical Care Medicine and to reduce hospital costs by monitoring patient flow in real-time. These efforts include the development of algorithms aimed at improving (a) compliance in the intensive care unit (ICU), (b) patient outcome, and (c) bedside care. In addition, we have developed algorithms to predict (i) the number of people who may show up to the emergency department in upcoming days, (ii) the likelihood that a patient will not show up to a medical appointment, (iii) a patient's length of stay after surgery or in the intensive care unit.
Figure. Stronger and more accurate prediction of how long a patient will stay in the Intensive Care Unit are obtained if you combine vital sign information with static clinical information.
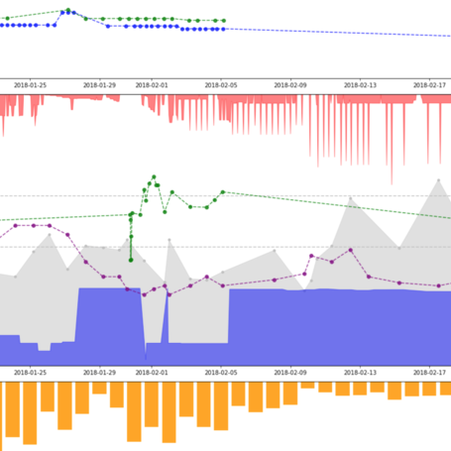
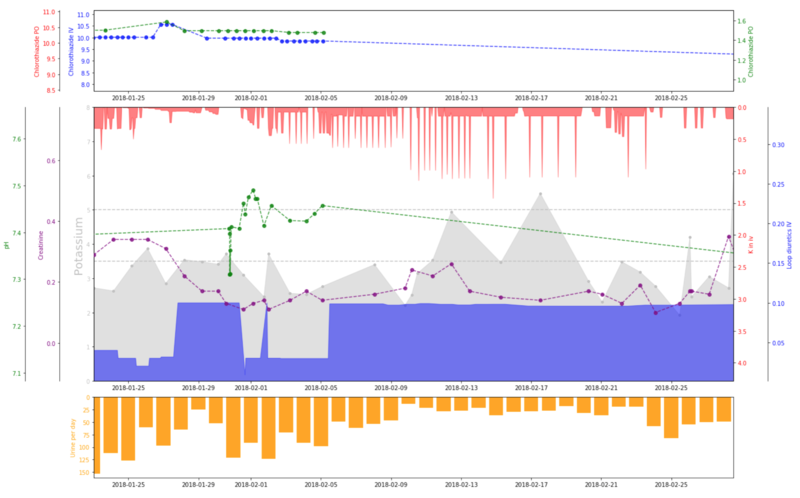
Figure. Real-time monitoring of potassium levels in Cardiac Intensive Care Units. Plot produced by Mathieu Molina
Expand
Placeholder for COVID States
Figure caption if needed
Expand
Understanding the global-scale dynamics of the chemical composition of our atmosphere is essential for addressing a wide range of environmental issues from air quality to climate change. Understanding this phenomenon enables us to evaluate and devise appropriate environmental policies, such as the Kyoto Protocol on global greenhouse gases emissions. Numerical modeling of global atmospheric chemical dynamics presents an enormous challenge associated with simulating hundreds of chemical species with time scales varying from milliseconds to years.
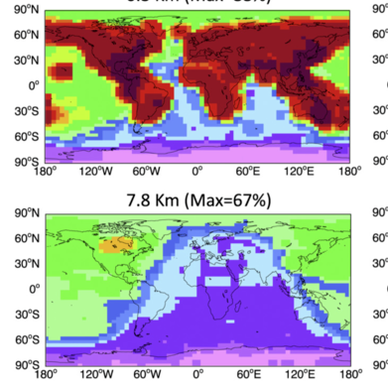
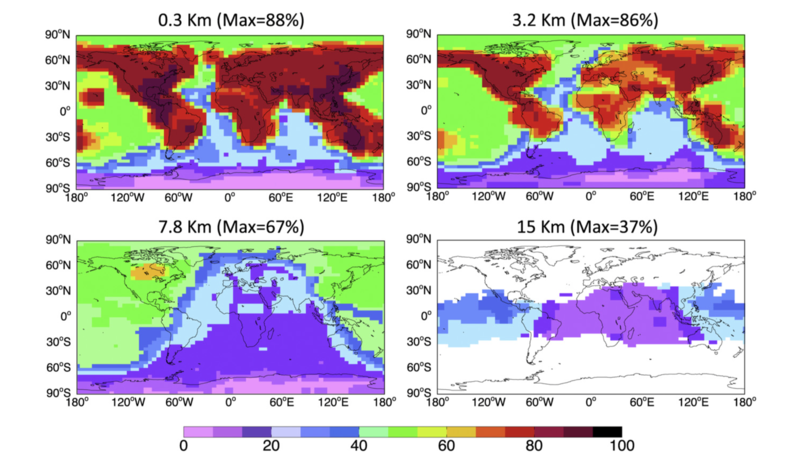
Our team has worked on the implementation of computationally efficient algorithms for calculating the time evolution of the concentration of chemical species in global 3-D models of atmospheric chemistry. We have also investigated the efficacy of adjoint based inverse modeling techniques for source attribution problems; and have assessed model errors and uncertainties. Figure. Percentage of fast species in the GEOS-Chem chemical mechanism at different altitudes using a threshold of d 1⁄4 102 molecules cm 3 s 1. White boxes in the bottom right panel are in the stratosphere. Results are for July 8, 2004 at 00 GMT. The full GEOS-Chem chemical mechanism includes 111 species to describe tropospheric ozone-NOx-VOC- aerosol chemistry. From: M. Santillana, P. Le Sager, D. J. Jacob, and M. P. Brenner. An adaptive reduction algorithm for efficient chemical calculations in global atmospheric chemistry models. Atmospheric Environment. Volume 44, Issue 35, pp 4426-4431, Nov 2010. (PDF)) |
Expand
The availability of on-line and real-time sources of big data sets gives us the opportunity to monitor how climate variables (among many other factors) influence the spread of Dengue, Antibiotic Resistance, and other outbreaks around the world
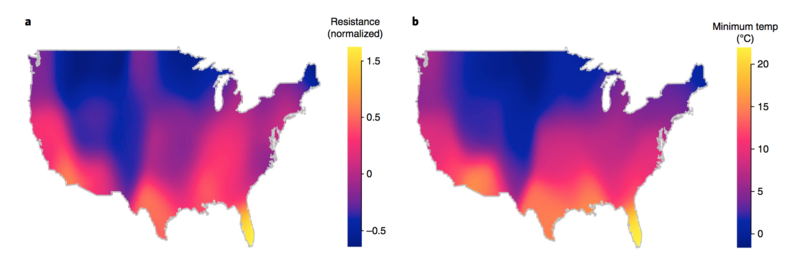
Figure. Antibiotic Resistant outbreaks across pathogens shown on the left panel and Minimum Air Temeprature on the right panel. From: MacFadden DR, McGough SF, Fisman D, Santillana M, Brownstein JS. Antibiotic Resistance Increases with Local Temperature Nature Climate Change 8 (2018), pp 510-514. (PDF)
Expand
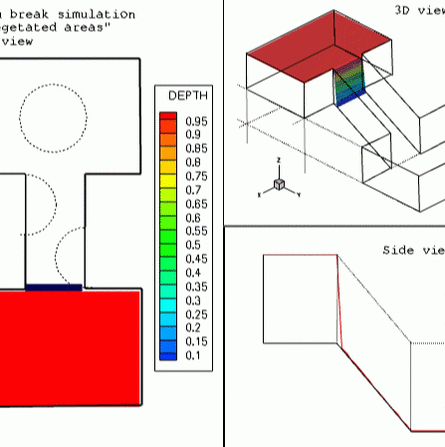
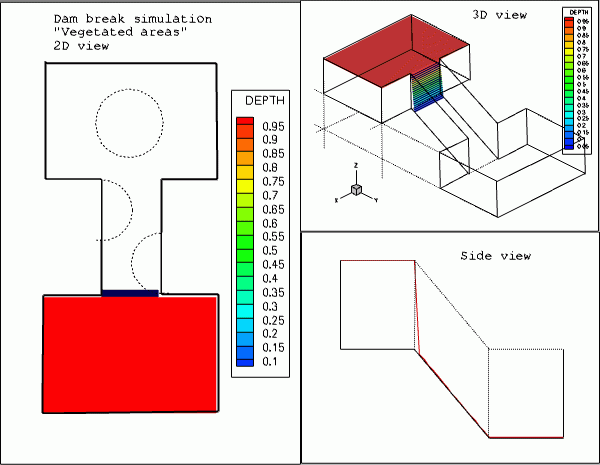
As a consequence of our changing climate, large efforts have been made to understand the social risks of storm surges (hypothesized to increase in frequency in warmer climate scenarios) and sea level rise in coastal areas. Of particular interest is the role that wetlands and coastal marshes play in storm surges and flooding events.
For example, coastal marshes and swamps act as a buffer zone between the Gulf of Mexico and inhabited inland areas in Louisiana, where an estimated 60-75 % of residents live within 50 miles of the coast (1993) and where, between 1899 and 1995, over a dozen major hurricanes (class 3-5) have hit (with the two most recent hits being the category 5 hurricanes Katrina and Rita in 2005). Understanding the role of these rich biological ecosystems in our changing climate requires the development of appropriate mathematical models. In our research, our team has studied analytically and numerically an effective equation often referred to in the literature as the diffusive wave approximation of the shallow water system of equations (DSW), used to simulate overland flow in wetlands and open channels. This equation is obtained by approximating the depth averaged continuity equations by empirical laws such as Manning’s or Chezy’s formulas and then combining the resulting expression with the free surface boundary condition. We have studied the properties of approximate (weak) solutions to the DSW using the continuous and discontinuous (LDG) Galerkin method, developing error estimates and implementing a 2-D code aimed at simulating water flow on experimental settings as well as real environments. We have also investigated inverse modeling approaches to estimate friction coefficients using the DSW as a physical model. Figure. Dam break numerical simulation |